永州陶铸中学2010年教师招聘考试数学试题

永州陶铸中学2010年教师招聘考试

数  学  试  题

一、选择题（在各小题给出的四个选项中，只有一项是符合题目要求的。本大题共10题，每题3分，计30分）

1、三峡工程在宜昌。三峡电站2009年发电798.5亿千瓦时，数据798.5亿用科学计数法表示为（    ）

A．798.5×10⁰亿　　　　　　B．79.85×10¹亿      

C．7.985×10²亿　　　　　　D．0.7985×10³亿

2、i 是虚数单位，复数

（   ）

A.1＋i          　　　   B.5＋5i           

C.-5-5i        　　　　  D.-1－i

3、函数f(x)=

的零点所在的一个区间是（   ）

A.（-2，-1）   　　    B.（-1,0）        

C.（0,1）   　  　　   D.（1,2）

4、甲、乙、丙、丁四人进行射箭测试，每人10次射箭成绩的平均数均是8

.9环，方差分别是

则成绩最稳定的是（   ）

A.甲   　　　 　      B.乙        

C.丙     　　　　　   D.丁

5、下列四个事件中，是随机事件（不确定事件）的为 (   )

A.颖颖上学经过十字路口时遇到绿灯

B.不透明袋中放了大小相同的一个乒乓球、二个玻璃球，从中去摸取出乒乓球

C.你这时正在解答本试卷的第12题

D.明天我县最高气温为60℃

 

 

 

 

6、如图，菱形ABCD中，AB=15,

°，则B、D两点之间的距离为（   ）

A.  15                 B.

C.  7.5                 D.15

 

 

 

 

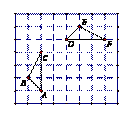
7、如图，在方格纸上△DEF是由△ABC绕定点P顺时针旋

转得到的。如果用（2,1）表示方格纸上A点的位置，（1,2）表示B点的位置，那么点P的位置为（    ）

A. (5,2)      　 B. (2,5)      C. (2,1)       D. (1,2)

 

 

 

 

 

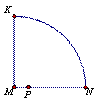
8、如图,在圆心角为90°的扇形MNK中，动点P从点M出发，沿MN

⌒NK

KM运动，最后回到点M的位置。设点P运动的路程为x，P与M两点之间的距离为y，其图象可能是（  ）。

	A.                B.                  C.                  D.

 

9、在△ABC中，内角A,B,C的对边分别是a,b,c，若

，

，则A=（    ）

A.

　　　　　B.

   　　　  C.

　　　　　　D.

 

 

 

 

 

 

 

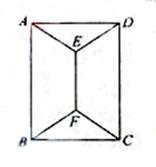
10、如图，用四种不同颜色给图中的A,B,C,D,E,F六个点涂色，要求每个点涂一种颜色，且图中每条线段的两个端点涂不同颜色，则不同的涂色方法用（    ）

A.288种    　　  B.264种       

C.240种     　   D.168种

 

 

 

 

 

 

 

二、填空题（本大题共4题，每题3分，计12分）

11、甲、乙两人在10天中每天加工零件的个数用茎叶图表示如下图，中间一列的数字表示零件个数的十位数，两边的数字表示零件个数的个位数，则这10天甲、乙两人日加工零件的平均数分别为          和        

12、下列各数

、

、

、

中最小的数是____________

13、如下图，PA与圆O相切于A，PCB为圆O的割线，且不过圆心O，已知

，则圆O的半径

14、已知数列

的前n项和为

，则这个数列的通项公式为____________.

三、解答题（本大题共5小题，共43分）

15、如图，华庆号船位于航海图上平面直角坐标系中的点A（10,2）处时，点C、海岛B的位置在y轴上，且

。

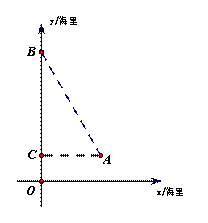
（1）求这时船A与海岛B之间的距离；

（2）若海岛B周围16海里内有海礁，华庆号船继续沿AC向C航行有无触礁危险？请说明理由（本题7分）

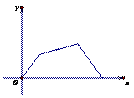
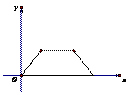
16、某市有A,B,C,D四个区。A区2003年销售了商品房2千套，从2003年到2007年销售套数（y）逐年（x）呈直线上升，A区销售套数2009年与2006年相等，2007年与2008年相等（如图①所示）；2009年四个区的销售情况如图②所示，且D区销售了2千套。

（1）求图②中D区所对扇形的圆心角的度数及2009年A区的销售套数；

 

 

 

 

 

 

 

 

 

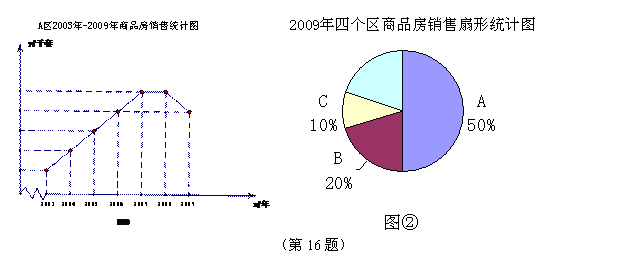
（2）求2008年A区的销售套数（本题8分）

17、给定双曲线

，过点A（2，1）的直线

与所给双曲线交于两点

、

，如果A点是弦

的中点，求

的方程。（本题8分）

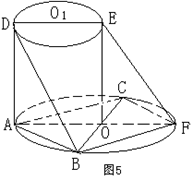
18、如图所示，AF、DE分别是⊙O、⊙O₁的直

径.AD与两圆所在的平面均垂直，AD＝8,BC是⊙O的直径，

AB＝AC＝6，OE//AD.

(Ⅰ)求二面角B—AD—F的大小；

(Ⅱ)求直线BD与EF所成的角.（本题10分）

19、已知函数

（Ⅰ）求函数

的单调区间和极值；

（Ⅱ）已知函数

的图象与函数

的图象关于直线

对称，证明当

时，

；

（Ⅲ）如果

，且

，证明

（本题10分）

c.#o@m

18

永州陶铸中学2010年教师招聘考试

数学试题参考答案

一、选择题（每小题3分，计30分）

　

二、填空题（本大题有4小题，每题3分，计12分）

11、 24;  33

12、

13、 7

14、

三、解答题（本大题有5小题，计43分）

15

．解：

（1）证明：∵∠CBA＝30°, ∠CAB＝60°，

90°．······ 1分

在Rt△ACB中, ∵

,

．······· 4分

（2）在Rt△ACB

中，tan60°=

，

,·········· 6分

（或BC≈17＞16）．··········· 7分

答：无触礁危险.

16．解：

（1）D区所对扇形的圆心角度数为：

．··· 2分

   2009年四个区的总销售套数为

（千套）.········ 3分

∴2009年A区的销售套数为

（千套）．········· 4分

  （2）∵从2003年到2007年A区商品房的销售套数（y）逐年（x）成直线上升

∴可设

．（或设

）·········· 5分

当

时，有

．

．

.········ 6分

当

时，

．（只写出y=6评1分）··········· 7分

∵2007、2008年销售量一样,

∴2008年销售量套数为6千套．················· 8分

17、解：

18、解  (Ⅰ)∵AD与两圆所在的平面均垂直,

∴AD⊥AB, AD⊥AF,故∠BAD是二面角B—AD—F的平面角，

依题意可知，ABCD是正方形，所以∠BAD＝45⁰.

即二面角B—AD—F的大小为45⁰.

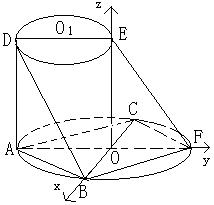
(Ⅱ)以O为原点，BC、AF、OE所在直线为坐标轴，建立空间直角坐标系（如图所示），则O（0，0，0），A（0，

，0），B（

，0，0）,D（0，

，8），E（0，0，8），F（0，

，0）

所以，

.

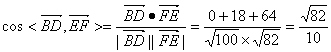
设异面直线BD与EF所成角为

，

则

直线BD与EF所成的角为

19、（Ⅰ）解：f’

令f’(x)=0,解得x=1

当x变化时，f’(x)，f(x)的变化情况如下表

X	( )	1	( )
f’(x)	+	0	-
f(x)		极大值

所以f(x)在(

)内是增函数，在(

)内是减函数。

函数f(x)在x=1处取得极大值f(1)且f(1)=

（Ⅱ）证明：由题意可知g(x)=f(2-x),得g(x)=(2-x)

令F(x)=f(x)-g(x),即

于是

当x>1时，2x-2>0,从而

’(x)>0,从而函数F（x）在[1,+∞)是增函数。

又F(1)=

F(x)>F(1)=0,即f(x)>g(x).

（Ⅲ)证明：（1）

若

（2）若

根据（1）（2）得

由（Ⅱ）可知，

>

,则

=

，所以

>

,从而

>

.因为

，所以

，又由（Ⅰ）可知函数f(x)在区间（-∞，1）内事增函数，所以

>

,即

>2.